Kvanttikohinaa emulaattorilla

Kubittien laadulla on suuri merkitys kvanttilaskun onnistumisen kannalta. Kohinasietokyky on tässä keskeinen, ehkä jopa tärkein parametri. Kvanttikohinalla tarkoitetaan erilaisia häiriöitä, jotka vaikuttavat kubittien kvanttitiloihin haitallisesti. Kohinaa syntyy esimerkiksi lämpötilasta, laitteiden epäpuhtauksista, värinästä, kosmisesta säteilystä ja magneettikentistä. Mitä paremmin kubitit sietävät ympäristöstä tulevia häiriöitä, sitä kauemmin ne pystyvät ylläpitämään kvanttitilojaan, ja sitä pidempiä ja monimutkaisempia laskuja niillä on mahdollista suorittaa.

Kohinan lisäksi myös epätarkkuus kvanttiporteissa lisää virheitä. Virtuaaliset kvanttiportit ovat fyysisiä operaatioita, joilla kubittien tiloja muokataan ja joilla kvanttilaskenta suoritetaan. Virheet kvanttiporteissa vaikuttavat laskun laatuun negatiivisesti, jopa turmellen sen kokonaan. Virheistä johtuen kvanttipiirien syvyys eli peräkkäisten kvanttiporttien määrä on rajoittunut.

Kvanttialgoritmien tutkimus ja kehitys ovat keskeisessä asemassa, jotta kvanttikoneista saadaan uutettua mahdollisimman paljon hyötyä mahdollisimman aikaisessa vaiheessa. CSC tarjoaa algoritmien mallintamiseen oivan ratkaisun: kvanttiemulaattori Kvasin, edistyneen Atos QLM kvanttiohjelmien kehitysympäristön. Emulaattorilla voidaan mallintaa kvanttialgoritmien toimintaa kohina ja muut kvanttitietokoneiden rajoitukset huomioiden. Kohinamallinnus kertoo, miten kvanttialgoritmit suoriutuvat oikeilla kvanttikoneilla, mikä mahdollistaa ongelmien välttämisen tai kiertämisen.

Seuraavassa tutustutaan kahteen tunnettuun, mutta hyvin erilaiseen kvanttialgoritmiin ja niiden kohinaherkkyyteen. Olisiko niiden avulla mahdollisuus saavuttaa kvanttihyötyä lähitulevaisuudessa?

Kvanttihyötyä likimääräisillä optimointialgoritmeilla

Kvantti-likimääräiset optimointialgoritmit (Quantum Approximate Optimization Algorithm, QAOA) kuuluvat hybridialgoritmien luokkaan. Hybridimallisessa HPC+QC laskennassa (High-Performance Computing + Quantum Computing), kvanttialgoritmit yhdistyvät perinteiseen laskentaan. Yksi tällainen ongelma on MaxCut, jossa verkon solmut jaetaan kahteen eri ryhmään niin, että eri ryhmään kuuluvien solmujen väliin jää mahdollisimman monta kaarta; toisin sanoen, maksimoidaan eri ryhmään kuuluvien naapurien määrä solmujen välillä (ks. kuva 1). 

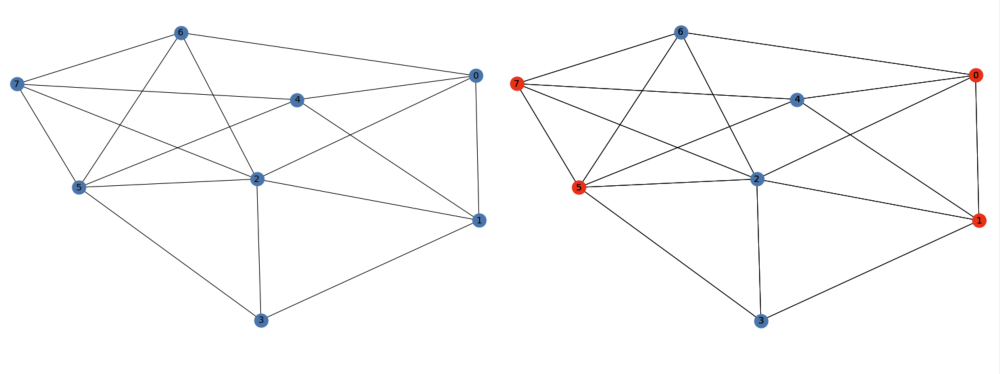
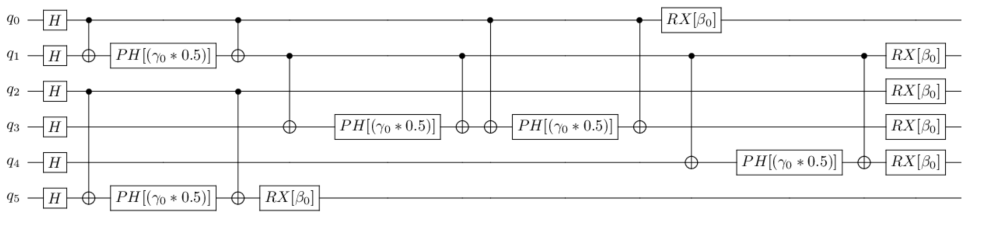
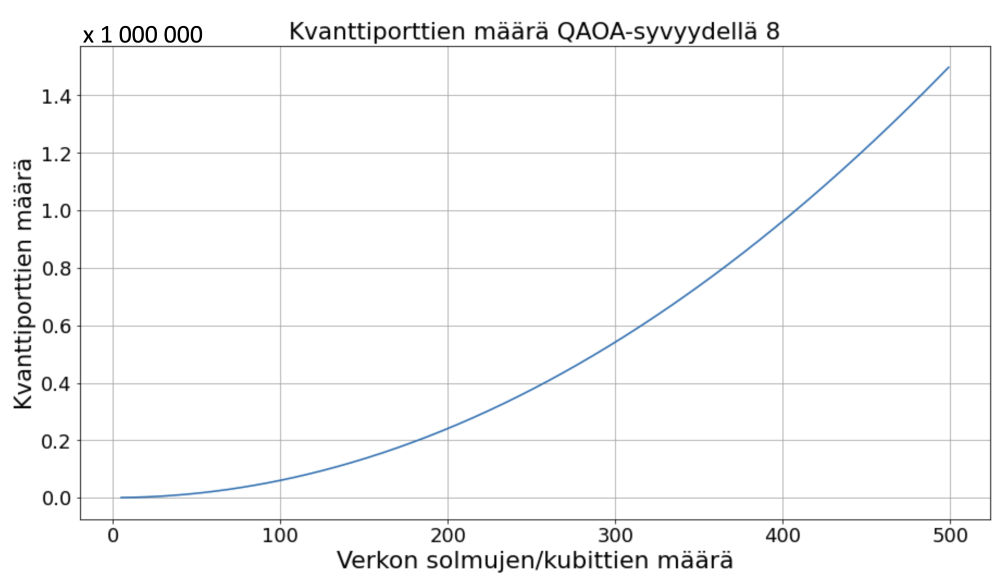
Ilman virheenkorjausta MaxCut ongelman ratkaisuun tarvittavien kubittien määrä riippuu pelkästään ongelmaverkon solmujen määrästä. Ongelmaksi muodostuukin piirien syvyys. Eräs kvantti-likimääräisien optimointialgoritmien ominaisuus on, että laskentaa suorittavan osio voidaan toistaa monta kertaa lisäämällä kvanttiportteja (ks. kuva 2). Jotta kvanttiratkaisun laskujen laatu vastaisi klassisia algoritmejä, olisi piirien laskeva osa toistettava vähintään kahdeksan kertaa (ks. Crooks, G). Jotta laskeminen kvanttikoneilla päihittäisi klassiset keinot, tulee kubittien määrää lisätä: verkkojen tulisi olla vähintään muutaman sadan solmun kokoisia. Kun lisätään kubitteja, kvanttipiirit syvenevät entisestään. Tämä tarkoittaa, että kvanttihyödyn saavuttamiseksi kvanttikoneen olisi pystyttävä suorittamaan yli miljoona kvanttioperaatiota (ks. kuva 3). Nykyisillä kvanttikoneilla kubittien kvanttiominaisuudet alkavat kuitenkin tuhoutua jo noin tuhannen kvanttiportin jälkeen.

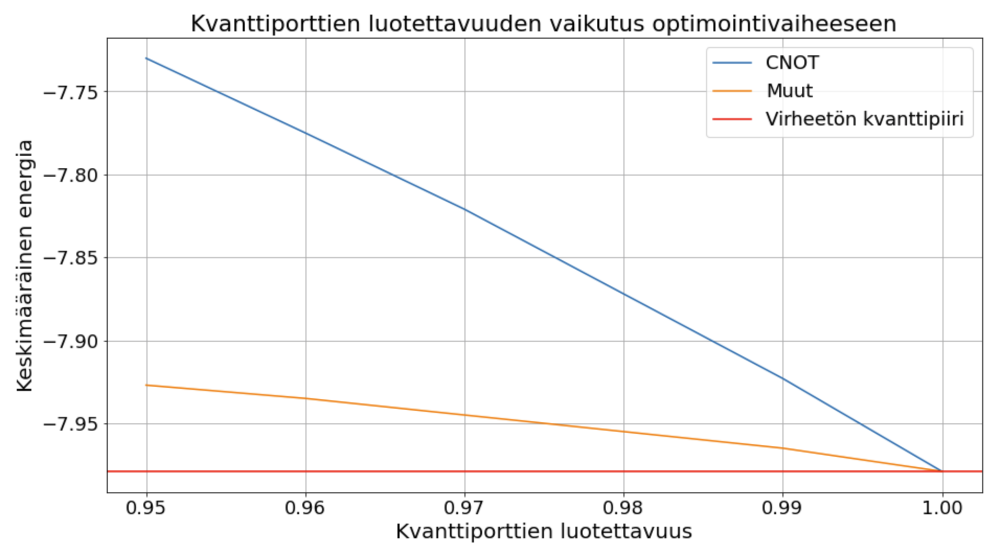
Virheellisten kvanttiporttien ja kohinan vaikutuksen tarkastelu paljastaa, että klassinen optimointivaihe kärsii enemmän virheellisistä kahden kubitin porteista kuin kaikista virheellisistä yhden kubitin porteista yhteensä (ks. kuva 4). Tarpeeksi laadukas ratkaisu saavutetaan pienemmällä todennäköisyydellä kuin täydellisesti toimivalla piirillä. Kyseistä algoritmia voi kuitenkin käyttää tämän kokoluokan verkoilla, ja se onkin toteutettu kokeellisesti 22:n solmun verkolle (ks. Harrigan, M. et al). Kvasilla kohinan mallinnus onnistuu vielä noin 20:n solmun verkoilla ja muutaman sadan kvanttiportin syvyydellä.

Pitkä matka kokonaislukujen alkulukutekijöiden löytämiseksi

Vuonna 1994 amerikkalainen matemaatikko Peter Shor kehitti algoritmin, jonka avulla kvanttitietokoneilla voidaan löytää suurien kokonaislukujen alkulukutekijät eksponentiaalisesti nopeammin kuin klassisilla koneilla (ks. Shor, P.). Tämä motivoi ja nopeutti kvanttiteknologian kehitystä, koska tämän kautta kvanttitietokoneilla voitaisiin rikkoa RSA julkisen avaimen salausmenetelmä, jolla suuri osa tietoliikenteestä salataan. RSA:n turvallisuus perustuu siihen, että klassisen laskennan keinoin suurten kokonaislukujen alkulukutekijöiden löytäminen kestäisi miljardeja vuosia. Shorin kvanttialgoritmi romahduttaa vaaditun laskenta-ajan.

Shorin algoritmin toteutus suurille luvuille on jo näköpiirissä, tosin vielä vain pilkahduksena horisontissa. Tarvittavien kubittien määrä riippuu salausavaimen pituudesta binäärimuodossa, joten esimerkiksi 2048-bittisen avaimen pituus on 2048. Tähän mennessä vähiten kubitteja käyttävä versio vaatii 2n +2 kubittia, missä n on luvun pituus (ks. Häner, S., Roeletter, M., Svore, K. M). Todellisuudessa tarvittavien kubittien määrä on paljon suurempi, sillä kubitteja tarvitaan myös virheenkorjausta varten. Onkin arvioitu, että 2048-bittisen salauksen purkaminen vaatisi noin 20 miljoonaa kubittia (ks. Gidney, C. and Ekerå, M).

Yksi Shorin algoritmin ominaisuus on, että se käyttää portteja, joita oikeat kvanttiprosessorit eivät pysty sellaisenaan suorittamaan. Nämä portit pitää purkaa operaatioiksi, joita prosessorin valikoimasta löytyy (ks. kuva 5). Esimerkiksi Shorin algoritmi luvulle 15 voidaan rakentaa 12 kubitilla ja näennäisesti noin 800 kvanttiportin voimin. Kuitenkin, kun portit purkaa useammaksi pienemmäksi portiksi, sellaisiksi joita kvanttitietokoneet pystyvät suorittamaan, tulee porttien määräksi noin 50 000.

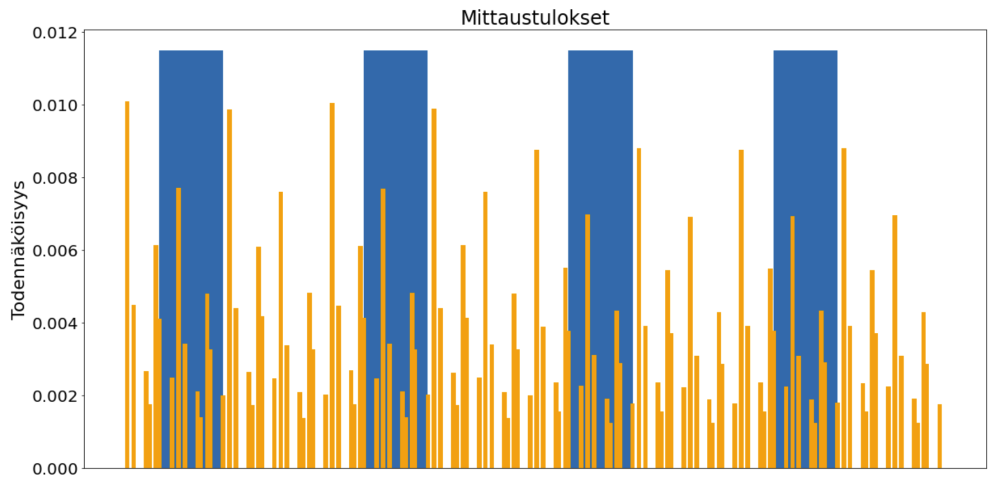
Kvasilla huomaa myös sen, kuinka tärkeä toimiva virheenkorjaus on algoritmin toiminnan kannalta. 50 000:n virheellisen portin ja kvanttikohinan jälkeen alkulukutekijöiden kannalta oikeiden kvanttitilojen määrä vähenee huomattavasti väärien kvanttitilojen määrään verrattuna, eikä laskusta ole juurikaan hyötyä (ks. kuva 6).

Yhteenveto

Jotta kvanttikoneilla voidaan tulevaisuudessa ratkoa ongelmia perinteisiä tietokoneita tehokkaammin, on kubittien oltava laadukkaampia ja kvanttiporttien tarkempia. Matalat algoritmit, jotka tarvitsevat suhteellisen pienen määrän kvanttiportteja, voivat silti olla hyödyllisiä jo muutaman vuoden sisällä. Kubittien määrän kasvaessa tarpeeksi suureksi, virheenkorjausmenetelmät voidaan ottaa käyttöön, jonka jälkeen yhä syvemmät ja leveämmät kvanttipiirit kasvattavat kvanttilaskennan mahdollisuuksia valtavasti.

Käsin kosketeltavaa

Työssä käytettyjä ja siihen liittyviä kvanttiohjelmia Jupyter Notebook muodossa löytyy CSC:n Githubin alta. Niitä voi ajaa ja muokata Kvasilla. https://github.com/CSCfi/Quantum/tree/main/Noise-modelling 
https://research.csc.fi/-/kvasi 

Termejä ja määritelmiä
Kubitti: Klassisen bitin kvanttivastine. Voi olla 1 ja 0 samanaikaisesti, superpositiossa.
Kvanttiportti: Operaatio eli alkeellisin ohjelmointikäsky jolla kubittia manipuloidaan.
Kvanttipiiri: Kubiteista ja kvanttiporteista muodostuva kokonaisuus, jolla kuvataan kvanttialgoritmi, jossa kvanttiportit suoritetaan järjestyksessä vasemmalta oikealle.
Kvanttihyöty: Kvanttihyöty saavutetaan, kun kvanttitietokoneella voidaan suorittaa käytännöllisesti hyödyllisiä laskuja klassisia koneita tehokkaammin.

Viitteet 

1. Crooks, G. (2018). Performance of the Quantum Approximate Optimization Algorithm on the Maximum Cut Problem. https://arxiv.org/abs/1811.08419 
2. Harrigan, M. et al. (2021). Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nature Physics, 17, 332-336. https://doi.org/10.1038/s41567-020-01105-y
3. Shor, P. (1997). Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing, 26, 1484-1509. https://doi.org/10.1137/S0097539795293172
4. Häner, S., Roeletter, M., Svore, K. M. (2017). Factoring using 2n+2 qubits with Toffoli based modular multiplication. https://arxiv.org/abs/1611.07995
5. Gidney, C. and Ekerå, M. (2021). How to factor 2048-bit RSA integers in 8 hours using 20 million noisy qubits. Quantum, 5, 433. https://doi.org/10.22331/q-2021-04-15-433

Joona Andersson
Kirjoittaja toimi harjoittelijana CSC:llä ja suuntaa seuraavaksi takaisin Aalto-yliopistoon kvanttiteknologian opintojen sekä uusien haasteiden pariin.

Mikael Johansson
Kirjoittaja tutkailee, pohtii ja mahdollistaa kvanttiteknologioita CSC:llä.