Required cookies

This website uses cookies necessary for its operation in order to provide the user with content and certain functionalities (e.g. language selection). You have no control over the use of these cookies.

Website visitor statistics

We collect visitor statistics on the use of the site. The data is not personally identifiable and is only stored in the Matomo visitor analytics tool managed by CSC.

By accepting visitor statistics, you allow Matomo to use various technologies, such as analytics cookies and web beacons, to collect statistics about your use of the site.

Change your cookie choices and read more about visitor statistics and cookies

CSC
Blog

Emulated quantum noise

In the future, quantum computing can solve certain tasks more efficiently than traditional computers; some problems are so complex that supercomputers in their classical form will never figure them out. This requires quantum computers that are considerably more powerful than current devices, however. The power of a quantum computer depends on both the number of qubits and their quality. Quality can be studied using CSC’s quantum computer emulator Kvasi.

Qubit quality is of great importance for the success of a quantum computation. Noise tolerance is a key, perhaps even the most important parameter here. Quantum noise refers to various perturbations that adversely affect the quantum states of qubits. Noise is generated by, for example, temperature, equipment contaminants, vibration, cosmic radiation, and magnetic fields. The better the qubits tolerate disturbances from the environment, the longer they will be able to maintain their quantum states, and the longer and more complex calculations they will be able to perform. In addition to noise, inaccuracies in quantum gates also increase errors. Virtual quantum gates are physical operations that modify the states of qubits and thereby perform the quantum computation. Errors in quantum gates negatively affect the quality of the calculation, even corrupting it completely. Due to the errors, the depth of the quantum circuits, i.e., the number of consecutive quantum gates is limited. 

Research and development of quantum algorithms are central for extracting maximum benefit from quantum computers at the earliest possible stage. CSC offers a splendid solution for modelling algorithms in the form of Kvasi, the advanced Atos QLM quantum programming environment. The emulator can be used to model the operation of quantum algorithms, considering noise and other limitations of quantum computers. Noise modelling tells us how quantum algorithms perform on real quantum computers, which makes it possible to avoid or circumvent problems. 

Next, we get acquainted with two well-known but very different quantum algorithms and their noise sensitivity. Could they provide quantum advantage in the near future? 

Quantum advantage with approximate optimization algorithms

Quantum Approximate Optimization Algorithms (QAOAs) belong to the category of hybrid algorithms. In hybrid HPC+QC computing (High-Performance Computing + Quantum Computing), quantum algorithms combine with traditional computing. One such problem is MaxCut, where the vertices of a network are divided into two different groups so that as many edges as possible remain between the vertices belonging to a different group; in other words, the number of neighbours belonging to a different group is maximized over all vertices (see Figure 1). 

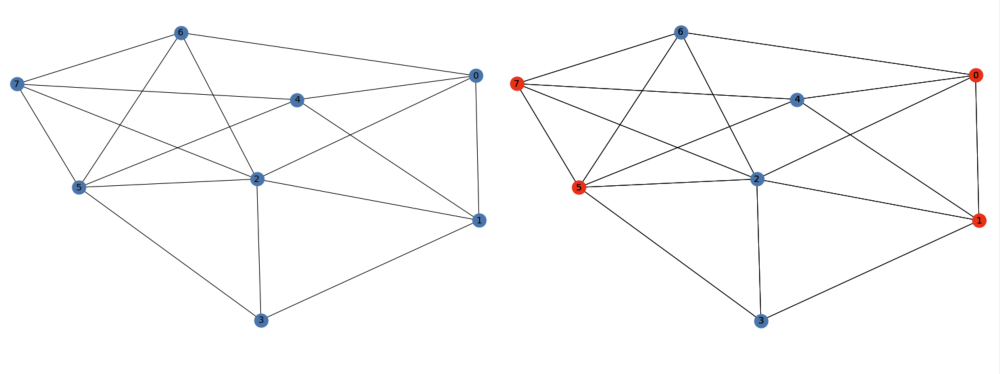
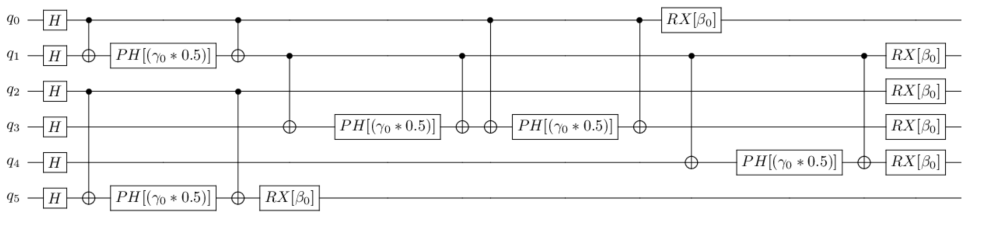
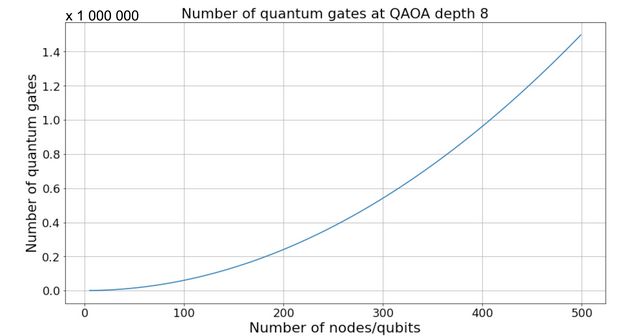
Figure 1. On the left is an example of a graph for which the task is to find “MaxCut”. There are eight vertices in this network, so the quantum algorithm requires eight qubits. On the right is the maximum cut for the same graph, as found using Kvasi. The value of MaxCut is 13 as there are thirteen edges connecting a red and a blue vertex.

Without error correction, the number of qubits needed to solve a MaxCut problem depends solely on the number of vertices in the graph. Circuit depth becomes the problem. One feature of quantum-approximate optimization algorithms is that the part performing the calculation can be repeated many times by adding quantum gates (see Figure 2). In order for the quality of the quantum solution to correspond to classical algorithms, the computing part of the circuits should be repeated at least eight times (see Crooks, G). In order for computation with quantum computers to beat classical means, the number of qubits must be increased: the graphs should be at least a few hundred vertices in size. As qubits are added, the quantum circuits deepen further. This means that to achieve quantum advantage, a quantum machine should be able to perform more than a million quantum operations (see Figure 3). However, with current quantum hardware, the quantum properties of qubits start to decay after about a thousand gate operations. 

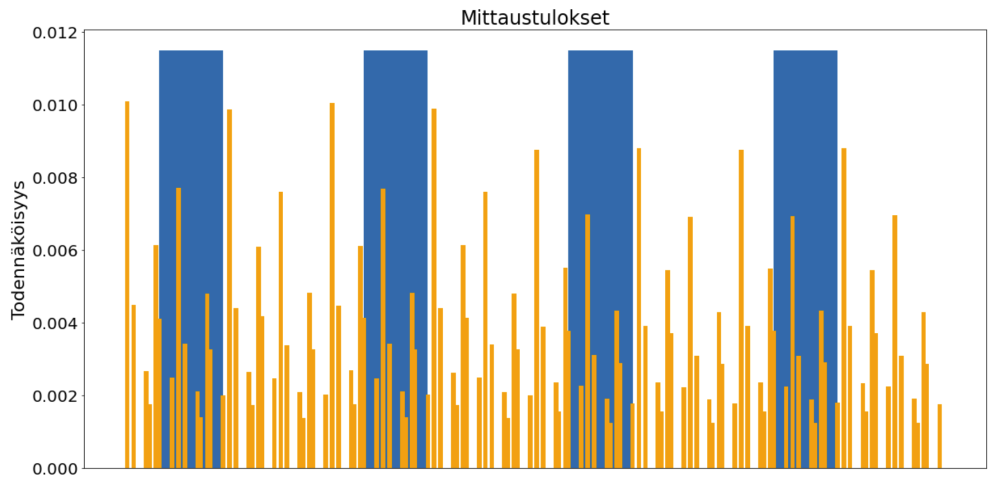
Figure 2. A QAOA circuit with six qubits. When increasing the depth, the gates following the Hadamard gates (H) are repeated several times. The PH and RX gates γ and β are classically optimised parameters.

Examination of the effect of inaccurate quantum gates and noise reveals that the classical optimization phase suffers more from erroneous two-qubit gates than from all erroneous single-qubit gates combined (see Figure 4). A solution of sufficient quality is less likely to be achieved than with a perfectly functioning circuit. However, the algorithm is applicable to networks of this size, and has been implemented experimentally for a 22-vertex network (see Harrigan, M. et al). On Kvasi, noise modelling is still possible with graphs of about 20 vertices and a depth of a few hundred quantum gates. 

Figure 3. Achieving quantum advantage is likely to require about 500 qubits, rapidly increasing the circuit depth to millions of gates.

Figure 4. Effect of gate errors on the quantum algorithm. The y-axis shows the expected value achieved by the optimisation, where a lower value is better. The x-axis describes the amount of gate error, where, for example, 0.97 means that the gate is working correctly with a 97% probability.

A long journey for finding the prime factors of integers 

In 1994, the American mathematician Peter Shor developed an algorithm that allows quantum computers to find prime factors for large integers exponentially faster than classical machines (see Shor, P.). This motivated and accelerated the development of quantum technology, as it would allow quantum computers to break the RSA public key encryption method, used to encrypt much of the internet traffic today. The safety of RSA is based on the fact that it would take billions of years to find the prime factors of large integers by classical computation. Shor’s quantum algorithm collapses the required computation time. 

The implementation of Shor’s algorithm for large numbers is already in sight, albeit just as a glimpse on the horizon. The number of qubits required depends on the length of the encryption key in binary form, so for example, the length of a 2048-bit key is 2048. To date, the algorithm with the lowest qubit cost requires 2n+2 qubits, where n is the length of the key (see Häner, S., Roeletter, M., Svore, K. M). In reality, the number of qubits required is much higher, as qubits are also needed for error correction. Indeed, it has been estimated that breaking the 2048-bit RSA encryption would require about 20 million qubits (see Gidney, C. and Ekerå, M). 

A feature of Shor’s algorithm is that it uses gates that real quantum processors cannot execute as is. These gates must be decomposed into operations that can be found in the processor’s native set (see Figure 5). For example, Shor’s algorithm for the number 15 can be built with 12 qubits and an apparent depth of about 800 quantum gates. However, when the gates are decomposed into the smaller operations that quantum computers can execute, the number of gates grows to about 50,000. 

Figure 5.  Many versions of Shor’s algorithm are based on three-qubit Toffoli gates, depicted on the left. On the right, one way to achieve the same effect using single- and two-qubit gates, to which most quantum processors are limited. 


On Kvasi, the importance of error correction for the correct operation of the algorithm becomes apparent. After 50,000 erroneous gates and quantum noise, the number of quantum states that lead to the correct prime factors is significantly reduced compared to the number of wrong quantum states, and the calculation is of little use (see Figure 6). 

Figure 6. Effect of noise on Shor’s algorithm. The blue bars represent noise-free results, three of which lead to the correct prime factors. Orange bars represent incorrect answers that result from noise.

Summary

In order for quantum computers to solve problems more efficiently than traditional computers in the future, the qubits must be of higher quality and the quantum gates more accurate. Shallow algorithms that require a relatively small number of quantum gates can, however, be useful within a few years. As the number of qubits grows large enough, error correction methods can be introduced, after which ever deeper and wider quantum circuits increase the possibilities of quantum computing tremendously. 

Tangible next steps

Quantum programs used for this work, and related ones, in the form of Jupyter Notebooks, are found on CSC’s Github. They can be run and edited with Kvasi.
https://github.com/CSCfi/Quantum/tree/main/Noise-modelling 
https://research.csc.fi/-/kvasi 

Terms and Definitions
Qubit: The quantum counterpart of the classical bit. Can be 1 and 0 simultaneously, in superposition.
Quantum gate: An operation, that is, the most basic of programming instructions for manipulating qubits.
Quantum circuit: An entity consisting of qubits and quantum gates that describes a quantum algorithm in which quantum gates are executed in order from left to right. 
Quantum advantage: Quantum advantage is achieved when a quantum computer can perform practically useful calculations more efficiently than classical machines.


References 

  1. Crooks, G. (2018). Performance of the Quantum Approximate Optimization Algorithm on the Maximum Cut Problem. https://arxiv.org/abs/1811.08419 
  2. Harrigan, M. et al. (2021). Quantum approximate optimization of non-planar graph problems on a planar superconducting processor. Nature Physics, 17, 332-336. https://doi.org/10.1038/s41567-020-01105-y
  3. Shor, P. (1997). Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM Journal on Computing, 26, 1484-1509. https://doi.org/10.1137/S0097539795293172
  4. Häner, S., Roeletter, M., Svore, K. M. (2017). Factoring using 2n+2 qubits with Toffoli based modular multiplication. https://arxiv.org/abs/1611.07995
  5. Gidney, C. and Ekerå, M. (2021). How to factor 2048-bit RSA integers in 8 hours using 20 million noisy qubits. Quantum, 5, 433. https://doi.org/10.22331/q-2021-04-15-433

Joona Andersson
The author worked as an intern at CSC and will next return to Aalto University to study quantum technology and tackle new challenges.

Mikael Johansson
The author explores, ponders, and enables quantum technologies at CSC.

High Performance ComputingQuantum Computing